Embark on a journey into the realm of geometry with Lesson 7-4 Parallel Lines and Proportional Parts Answer Key. This comprehensive guide unveils the intricacies of parallel lines and their remarkable relationship with proportional parts, empowering you to conquer mathematical challenges with precision and confidence.
Delve into the world of parallel lines, where their unwavering parallelism governs the formation of proportional parts. Discover how these concepts intertwine to solve real-world problems and unlock the secrets of everyday geometry.
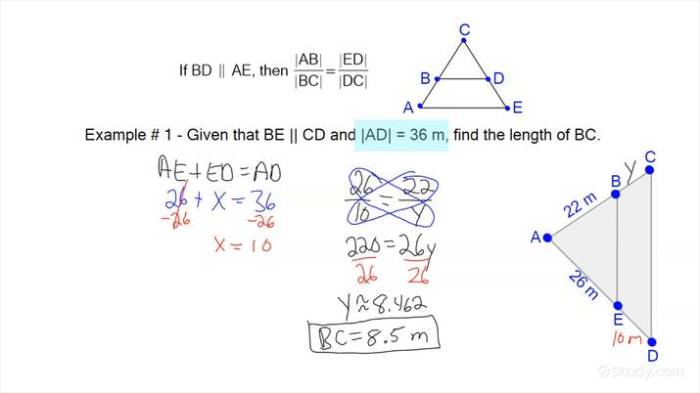
Understanding Parallel Lines and Proportional Parts

In geometry, parallel lines are lines that never intersect. Proportional parts refer to the relationship between corresponding parts of two similar figures. The concept of parallel lines and proportional parts is fundamental in geometry and has various applications in real-world scenarios.
Relationship between Parallel Lines and Proportional Parts
When two parallel lines are intersected by a transversal (a line that intersects both parallel lines), the corresponding angles formed are congruent. This relationship leads to the formation of proportional parts, where the ratios of the lengths of the segments created by the transversal on the parallel lines are equal.
For example, if two parallel lines are intersected by a transversal, the ratio of the length of the segment on one line between the points of intersection to the length of the corresponding segment on the other line is the same.
This property is known as the intercept theorem.
Applications in Real-World Scenarios, Lesson 7-4 parallel lines and proportional parts answer key
The concept of parallel lines and proportional parts has numerous practical applications in various fields:
- Architecture:Used to design buildings and structures with proportional dimensions, ensuring aesthetic appeal and structural integrity.
- Engineering:Applied in designing bridges, roads, and other infrastructure to ensure stability and load distribution.
- Art and Design:Used to create visually appealing and harmonious compositions in paintings, sculptures, and other artistic works.
Top FAQs: Lesson 7-4 Parallel Lines And Proportional Parts Answer Key
What is the relationship between parallel lines and proportional parts?
Parallel lines create proportional parts when they intersect transversals, forming similar triangles with equal ratios of corresponding sides.
How can I use parallel lines and proportional parts to solve problems?
Identify parallel lines and transversals, establish proportions between corresponding segments, and solve for unknown lengths or ratios.
What are some real-world applications of parallel lines and proportional parts?
Engineering, architecture, design, surveying, and navigation all utilize parallel lines and proportional parts for accurate measurements and calculations.